STRUKTUR DATA – TREE.

Apa itu TREE ..?

Tree adalah salah satu bentuk struktur data tidak linier yang menggambarkan hubungan yang menggambarkan hubungan yang bersifat hirarkis (hubungan one to many) antara elemen – elemen. Tree bisa didefinisikan sebagai kumpulan simpul/node.

Ada 2 macam tree , yaitu Tree Statik dan Tree Dinamik.

1.       Tree Statik

Adalah isi node nya tetap karena bentuk pohonnya sudahdi tentukan.

2.       Tree Dinamik

Adalah isi node nya berubah ubah karena proses penambahan dan penghapusan.

Contoh penggunaan Tree :

a.       Silsilah Keluarga.

b.       Parse Tree (pada kompiler)

c.       Struktur File

d.       Pertandingan

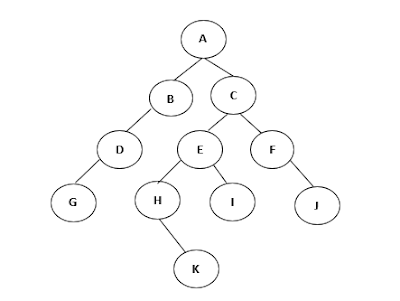
Contoh TREE :

Istilah dalam TREE.

   1.       Predesesor = Node yang berada diatas node tertentu.

(contoh :  B predesesor dari B dan C).

   

   2.       Succesor = Node yang berada dibawah node tertentu.
c                       contoh :  B dan C merupakan succesor dari A).

    3.       Ancestor = Seluruh node yang terletak sebelum node tertentu dan terletak pada jalur yang sama.                           (contoh :  D merupakan Ancestor dari C dan A).

    4.       Parent = Predesesor satu level diatas satu node
                      (contoh : C merupakan parent dari D,E,F).

    5.       Child = Succesor satu level dibawah satu node
                    (contoh : C merupakan child dari D,E,F)

    6.       Sibling = Node yang memiliki parent yang sama
                       (contoh :D,E,F merupakan Sibling)

    7.       Subtree = Bagian dari tree yang berupa suatu node beserta descendant-nya
                        (contoh : Subtree B, E, F dan Subtree  D, G, H)

    8.       Size = Banyaknya node dalam suatu tree
                   (contoh : gambar tree diatas memiliki size = 10)

    9.       Height = Banyaknya tingkat/level dalam suatu tree

                (contoh : gambar tree diatas memiliki height = 4)

    10.   Root (Akar) = Node khusus dalam tree yang tidak memiliki predesesor

                        (Contoh : A)

    11.   Leaf (Daun) = Node-node dalam tree yang tidak memiliki daun

                        (contoh : D,I,J,F,G,H)

    12.   Degree (Derajat) = Banyaknya child yang dimiliki oleh suatu node

                                (contoh : Node B memiliki derajat 2, node C memiliki derajat 3)

Penulisan Tree dalam Array :

-          Index ke-0 merupakan Root

-          Cara mencari indeks dari Left Child adalah

 

 Keterangan : P adalah Indeks atau Parent.

-          Cara mencari indeks dari Right Child adalah

 

Keterangan : P adalah Indeks atau Parent.

Contoh mengubah Tree ke dalam bentuk Array.

LEFT CHILD (2P + 1)                                                                         RIGHT CHILD (2P + 2)

B = 2P + 1                                                                                            C = 2P + 2

    = 2(0) + 1                                                                                             = 2(0) + 2

    = 1 (terletak di Indeks 1)                                                                      = 2 (terletak di Indeks 2)

D = 2P + 1                                                                                             F = 2P + 2

    = 2(1) + 1                                                                                              = 2(2) + 2

    = 3 (terletak di Indeks 3)                                                                       = 6 (terletak di Indeks 6)

E = 2P + 1                                                                                               I = 2P + 2

   = 2(2) + 1                                                                                               = 2(5) + 2

   = 5 (terletak di Indeks 5)                                                                        = 12 (terletak di Indeks 12)

G = 2P + 1                                                                                               J = 2P + 2

   = 2(3) + 1                                                                                                = 2(6) + 2

   = 7 (terletak di Indeks 7)                                                                         = 14 (terletak di Indeks 14)

H = 2P + 1                                                                                                K = 2P + 2

    = 2(5) + 1                                                                                                 = 2(11) + 2

    = 11 (terletak di Indeks 11)                                                                      = 24 (terletak di Indeks 24)

Hasil :

Demikian penjelasan tentang TREE ya guyss !!!

Semoga bermanfaat J J